単純ランダムウォークとは？分かりやすく解説！

単純ランダムウォークの概要

最も単純なランダムウォークのモデル

一定時間ごとに$+1$、又は$-1$だけ移動する千鳥足の酔っ払いを考えてみます。完全にランダムに動くものとします。

例えば、次のように動いたとします。

$-1,+1,+1,+1,+1,-1,+1,-1+1,-1-1$

この時、それぞれの動きを確率変数と捉えることができます。

$X_1=-1, X_2=+1, X_3=+1, X_4=+1, X_5=+1, X_6=-1,…$

このような確率変数の並びを確率過程と呼びます。

n歩目に酔っ払いはどこにいるのか？

酔っ払いの位置は、確率変数の総和で決まります。

$0$歩目　⇒　$0$
$1$歩目　⇒　$-1$
$2$歩目　⇒　$-1+1=0$
$3$歩目　⇒　$-1+1+1=+1$
$4$歩目　⇒　$-1+1+1+1=+2$
：

$n=0$だと$0$、$n=4$だと初期位置から$+2$の位置にいます。
このようにして得られた離散的な時系列を「単純ランダムウォーク」と呼称します。

単純ランダムウォークの期待値と分散

期待値

それぞれの確率変数は、$+1$か$-1$のどちらかしか取りません。ここで、$+1$を取る確率$p=0.7$、$-1$を取る確率$q=0.3$と置きます。

このような仮定を置くと、$n$歩目にどこの位置にいるかはある程度予測することができます。$+1$を取って前に進む可能性の方が高いため、時間が長くなるにつれ前に進んでいく傾向になりそうです。

酔っ払いの位置は、確率変数の総和によって決まるため、$n$歩目の総和を$S_n$と置きます。$S_n$の期待値$E(S_n)$はどうなるのでしょうか。

$E(S_n)=E(X_1+X_2+X_3+X_4…X_n)$

期待値の性質から「和の期待値=期待値の和」であるため、

$E(S_n)=E(X_1+X_2+X_3+X_4…X_n)$
$=E(X_1)+E(X_2)+E(X_3)+E(X_4)…E(X_n)$

ここで例えば期待値$E(X_1)$を考えると、

$E(X_1)=+1×p+(-1)×q$
$=p-q$$…(1)$

であり、それぞれの期待値は同じ確率変数と確率分布を持つ等価なものであるから、

$E(S_n)=E(X_1)+E(X_2)+E(X_3)+E(X_4)…E(X_n)$
$=nE(X)$
$=n(p-q)$

$p=0.7,q=0.3$を代入すると、

$E(S_n)=n(p-q)$
$=n(0.7-0.3)$
$=n×0.4$

歩数が多くなると徐々に前に進んでいくことが分かりました。

分散

$n$歩目の酔っ払いの位置の分散を考えます。

$V(S_n)=V(X_1+X_2+X_3+X_4…X_n)$

確率変数が独立であれば「和の分散=分散の和」であるから、

$V(S_n)=V(X_1+X_2+X_3+X_4…X_n)$
$=V(X_1)+V(X_2)+V(X_3)+V(X_4)…V(X_n)$

ここでそれぞれの分散は等価であるから、

$V(S_n)=V(X_1)+V(X_2)+V(X_3)+V(X_4)…V(X_n)$
$=nV(X)$$…(2)$

次の公式を利用して分散$V(X)$を求めます。
なお、分散の定義式から当該公式の導出はページの末尾に参考として記載いたします。

$V(X)=E(X^2)-\{E(X)\}^2$$…(3)$

$X$は$+1,-1$しか取らないため、$X^2$は必ず$1$になる。よって、$(3)$の$E(X^2)$の項は次の通りとなる。

$E(X^2)=X^2×p+X^2×q$
$=(+1)^2×0.7+(-1)^2×0.3=1$

この計算結果と$(1)$を、$(3)$の式に代入すると、

$V(X)=1-(p-q)^2$

$q=1-p$であるため、

$=1-(p-(1-p))^2$
$=1-(p-1+p)^2$
$=1-(2p-1)^2$
$=1-(4p^2-4p+1)$
$=-4p^2+4p$
$=4p-4p^2$
$=4p(1-p)$
$=4pq$$…(4)$

$(4)$の計算結果を、$(2)$に代入します。

$V(S_n)=4npq$

$p=0.7,q=0.3$を代入すると、

$V(S_n)=4n×0.7×0.3$

分散も、歩数が進むにつれて大きくなることが分かりました。

単純ランダムウォークのグラフ

$p=0.7$でプロット

エクセルで乱数を生成し、$p=0.7$で複数のグラフをプロットしてみました。

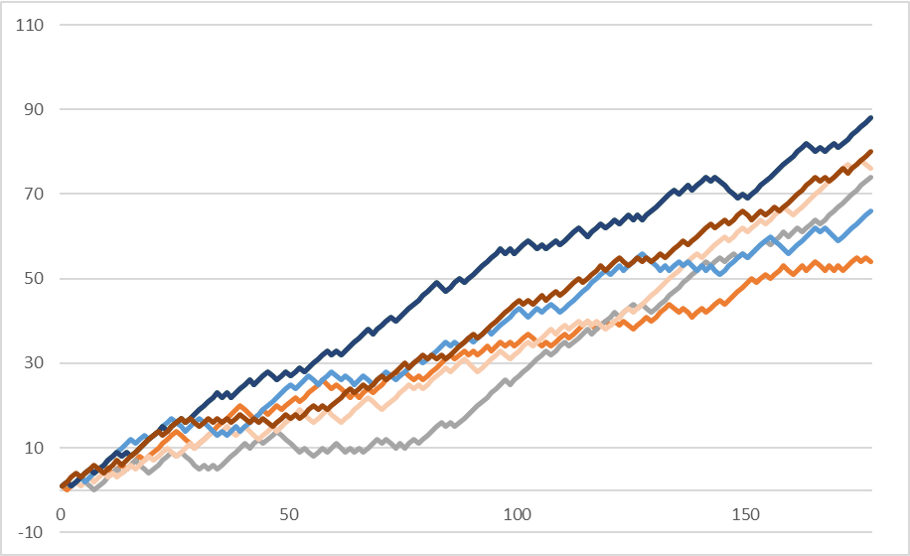
ランダムウォークの特徴

短期的には予測不可能なランダムな動きをしながらも、長期的には$p=0.7$の方向性に推移していることが分かります。また、時間経過と共にブレも大きくなっており、分散が逓増しています。

株価の動きも、短期的には一切の予測が不可能なランダムウォークですが、長期的には株式発行企業の業績に基づいて推移するといわれております。そのため、ランダムウォークは株価の動きを擬制するのに適しており、一般的な株価モデルはランダムウォークの考え方から導かれています。

補足

使用した分散の公式の導出

分散は平均値との差を取って二乗したものなので次の式で表すことができます。

$V(X)=E((X-μ)^2)$

$V(X)=E((X-μ)^2)$
$=E(X^2-2μX+μ^2)$

期待値の性質から「和の期待値＝期待値の和」なので、

$=E(X^2-2μX+μ^2)$
$=E(X^2)-E(2μX)+E(μ^2)$

期待値の性質から定数は外に出せるため、

$=E(X^2)-E(2μX)+E(μ^2)$
$=E(X^2)-2μE(X)+E(μ^2)$

$E(μ^2)$の項に着目すると、$μ$は確率変数ではなく定数なので100%$μ^2$の値しか取らず、期待値も$E(μ^2)=μ^2$となります。また、$μ=E(X)$なので、

$=E(X^2)-2μE(X)+E(μ^2)$
$=E(X^2)-2μ×μ+μ^2$
$=E(X^2)-2μ^2+μ^2$
$=E(X^2)-μ^2$
$=E(X^2)-\{E(X)\}^2$