モーメントとは?
確率分布を把握するための必要な要素
確率分布は正規分布のような形状をとっていないことも多くあります。この時、形状の特徴を把握するために求めるのがモーメントです。
モーメントの定義
原点付近のn次のモーメントは次の通りで、積率と呼称されます。
\[μ_n=E(X^n)\]
平均周りのn次のモーメントは次の通りです。
\[μ´_n=E\{(X-μ)^n\}\]
確率変数を1回乗じて算出する期待値は、1次モーメント$μ_1$であると言えますし、分散は2次モーメント$μ´_2$です。
標準正規分布のモーメントを求める
標準正規分布の確率密度関数
正規分布は次の式で表されます。
\[f(x)=\frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{(x-μ)^2}{2\sigma^2}}\]
標準正規分布は平均0、分散1の正規分布なので、$μ=0$、$\sigma^2=1$を代入すると次式となります。
\[f(x)=\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}\]
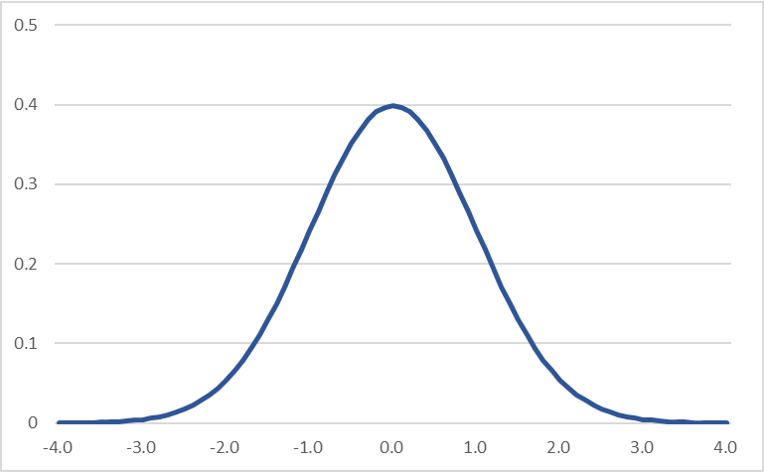
標準正規分布の1次モーメント
確率密度関数に確率変数を1回掛けたものが、1次モーメント(期待値)の定義式です。
\[E(X^1)=\displaystyle \int_{-\infty}^{\infty}x^1×\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}dx\]
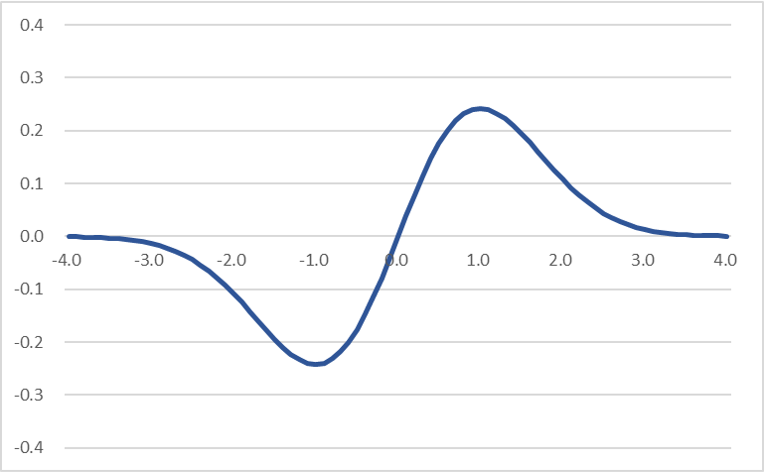
ゼロを境界にして正負が反転した左右対称になっているため、1次モーメント(期待値)を計算すればゼロになる事が分かります。
標準正規分布の2次モーメント
\[E(X^2)=\displaystyle \int_{-\infty}^{\infty}x^2×\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}dx\]
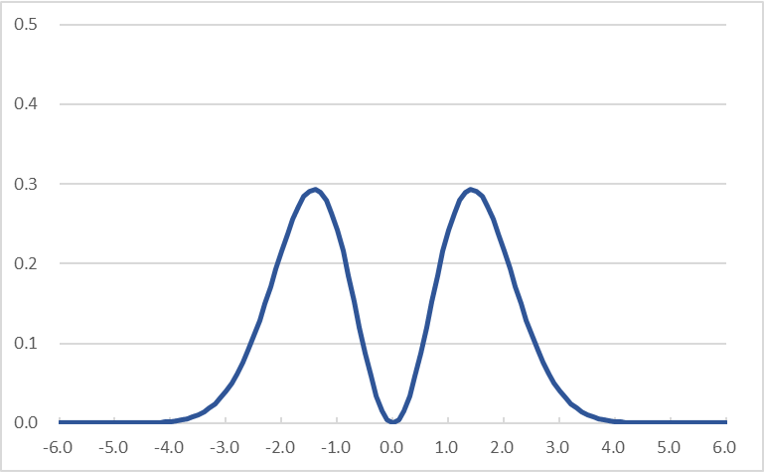
後述の「標準正規分布の4次モーメント」で詳細な計算過程を記述しています。同様の計算方法で2次モーメントは1と求めることができます。
標準正規分布の3次モーメント
\[E(X^3)=\displaystyle \int_{-\infty}^{\infty}x^3×\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}dx\]
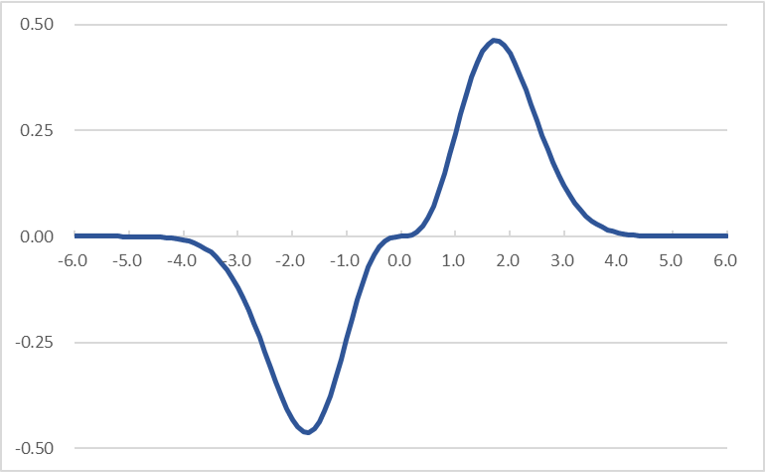
グラフにしてプロットすると、奇数モーメントはゼロになる事が明白です。
標準正規分布の4次モーメント
\[E(X^4)=\displaystyle \int_{-\infty}^{\infty}x^4×\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}dx\]
$=\frac{1}{\sqrt{2\pi}}\displaystyle \int_{-\infty}^{\infty}x^4×e^{-\frac{x^2}{2}}$
部分積分の公式$\displaystyle \int_{-\infty}^{\infty}f(x)g(x)dx=f(x)G(x)-\displaystyle \int_{-\infty}^{\infty}f´(x)G(x)dx$を使います。
$f(x)=x^3$
$g(x)=x×e^{-\frac{x^2}{2}}$
$g(x)$は積分する必要がありますので、その際後の$(3)$の計算が簡単になるよう調整し$x$をつけます。
先に$G(x)$を計算します。
$G(x)=\displaystyle \int x×e^{-\frac{x^2}{2}}dx$
置換積分を使用し、$t={-\frac{x^2}{2}}$と置きます。
$G(x)=\displaystyle \int x×e^tdx$$ …(1)$
このままでは解けないため、tを微分して代入します。
$t={-\frac{x^2}{2}}$
$t=-\frac{1}{2}x^2$
$\frac{dt}{dx}=-x$
$dx=-\frac{1}{x}dt$$ …(2)$
(2)を(1)に代入します。
$G(x)=\displaystyle \int x×e^t×-\frac{1}{x}dt$$ …(3)$
$=\displaystyle \int -e^tdt=-e^t$
ネイピア数なので積分しても変わらない。$t$を$x$に戻す。
$G(x)=-e^{-\frac{x^2}{2}}$$ …(4)$
部分積分の公式$\displaystyle \int_{-\infty}^{\infty}f(x)g(x)dx=f(x)G(x)-\displaystyle \int_{-\infty}^{\infty}f´(x)G(x)dx$に代入していきます。
$\frac{1}{\sqrt{2\pi}}\displaystyle \int_{-\infty}^{\infty}x^3・x×e^{-\frac{x^2}{2}}dx=\frac{1}{\sqrt{2\pi}}\{x^3・-e^{-\frac{x^2}{2}}-\displaystyle \int_{-\infty}^{\infty}3x^2・-e^{-\frac{x^2}{2}}dx\}$
$=-\frac{1}{\sqrt{2\pi}}\{x^3・e^{-\frac{x^2}{2}}\}+3・\frac{1}{\sqrt{2\pi}}\{\displaystyle \int_{-\infty}^{\infty}x^2・e^{-\frac{x^2}{2}}dx\}$
$\{x^3・e^{-\frac{x^2}{2}}\}$という関数に着目すると、$x$が極限に近づいたとき、$e^{-\frac{x^2}{2}}$が小さくなるスピードが$x^3$が大きくなるスピードより速いため無限遠でゼロに収束して次のグラフとなり、積分全体に対する影響は無視できるほど小さいと評価できるため、第1項はゼロとなる。
$=3・\frac{1}{\sqrt{2\pi}}\{\displaystyle \int_{-\infty}^{\infty}x^2・e^{-\frac{x^2}{2}}dx\}$$…(5)$
(5)は、積分がそのままでは解けないので、再度部分積分を使用する。
$f(x)=x$
$g(x)=x×e^{-\frac{x^2}{2}}$
前回の置換積分と$g(x)$の定義が同じであるため、(4)を使用してこの部分積分を解くと、
$\displaystyle \int_{-\infty}^{\infty}x^2・e^{-\frac{x^2}{2}}dx=x・-e^{-\frac{x^2}{2}}-\displaystyle \int_{-\infty}^{\infty}1・-e^{-\frac{x^2}{2}}dx$
$=x・-e^{-\frac{x^2}{2}}+\displaystyle \int_{-\infty}^{\infty}e^{-\frac{x^2}{2}}dx$
やはり、第1項はゼロになるため、
$=\displaystyle \int_{-\infty}^{\infty}e^{-\frac{x^2}{2}}dx$$ …(6)$
ガウス積分の関連公式$\displaystyle \int_{-\infty}^{\infty}e^{-ax^2}=\sqrt{\frac{\pi}{a}}$を使用して(6)を解く。
$=\sqrt{\frac{\pi}{\frac{1}{2}}}$
$=\sqrt{2\pi}$$ …(7)$
(7)を(5)の右側に戻すと、
$=3・\frac{1}{\sqrt{2\pi}}\{\sqrt{2\pi}\}$
$=3$
標準正規分布の4次モーメントは3になる事が分かりました。
モーメントの性質
奇数モーメント
奇数モーメントはゼロを境界に正負が反転している形状であるため、積分するとゼロになる事が明らかでした。
偶数モーメント
偶数モーメントは、乗数が増えると部分積分の計算工程がその分繰り返されることになります。よって、二重階乗によって置き換えることが可能であり、偶数モーメントは次式で求めることができます。
\[E(X^n)=\frac{n!}{2^k・k!} n=2k,k=0,1,2,3,4,5,,,,\]
この公式は、ブラックショールズ方程式の導出過程で、テイラー展開から伊藤のレンマを導くために利用します。以下に当該公式の導出過程を示します。
\[E(X^n)=\displaystyle \int_{-\infty}^{\infty}x^n×\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}dx\]
$=\frac{1}{\sqrt{2\pi}}\displaystyle \int_{-\infty}^{\infty}x^n×e^{-\frac{x^2}{2}}$
4次モーメントを求めた時と同様に、部分積分を使用します。
$f(x)=x^{n-1}$
$g(x)=x×e^{-\frac{x^2}{2}}$
$f´(x)=(n-1)x^{n-2}$
$G(x)=-e^{-\frac{x^2}{2}}$
$\frac{1}{\sqrt{2\pi}}\displaystyle \int_{-\infty}^{\infty}x^{n-1}・x×e^{-\frac{x^2}{2}}dx=\frac{1}{\sqrt{2\pi}}\{x^{n-1}・-e^{-\frac{x^2}{2}}-\displaystyle \int_{-\infty}^{\infty}(n-1)x^{n-2}・-e^{-\frac{x^2}{2}}dx\}$
$=-\frac{1}{\sqrt{2\pi}}\{x^{n-1}・e^{-\frac{x^2}{2}}\}+(n-1)・\frac{1}{\sqrt{2\pi}}\{\displaystyle \int_{-\infty}^{\infty}x^{n-2}・e^{-\frac{x^2}{2}}dx\}$
$=(n-1)・\frac{1}{\sqrt{2\pi}}\{\displaystyle \int_{-\infty}^{\infty}x^{n-2}・e^{-\frac{x^2}{2}}dx\}$$ …(8)$
ここで、$(8)$の$(n-1)$を除く右側は、$E(X^{n-2})$の定義式に他ならないため、
$E(X^n)=(n-1)E(X^{n-2})$$ …(9)$
と置くことができる。同様の計算を繰り返すと、
$E(X^{n-2})=(n-3)E(X^{n-4})$
$E(X^{n-4})=(n-5)E(X^{n-6})$
となるため、これらを$(9)$に代入する。
$E(X^n)=(n-1)(n-3)(n-5)…E(X^2)$
nは偶数であるため、最終的にE(X^2)に行き着く。
2次モーメント$E(X^2)$は計算すると1であるため、次の通り2重階乗となります。
$E(X^n)=(n-1)(n-3)(n-5)…1$
この式は$n$が偶数の時しか成り立たないため、正しく記載すると初めに示した公式になります。
\[E(X^n)=\frac{n!}{2^k・k!} n=2k,k=0,1,2,3,4,5,,,,\]

