基礎データの準備
Yahooファイナンスから株価情報をダウンロード
Yahooファイナンスから株価情報をダウンロードできました。
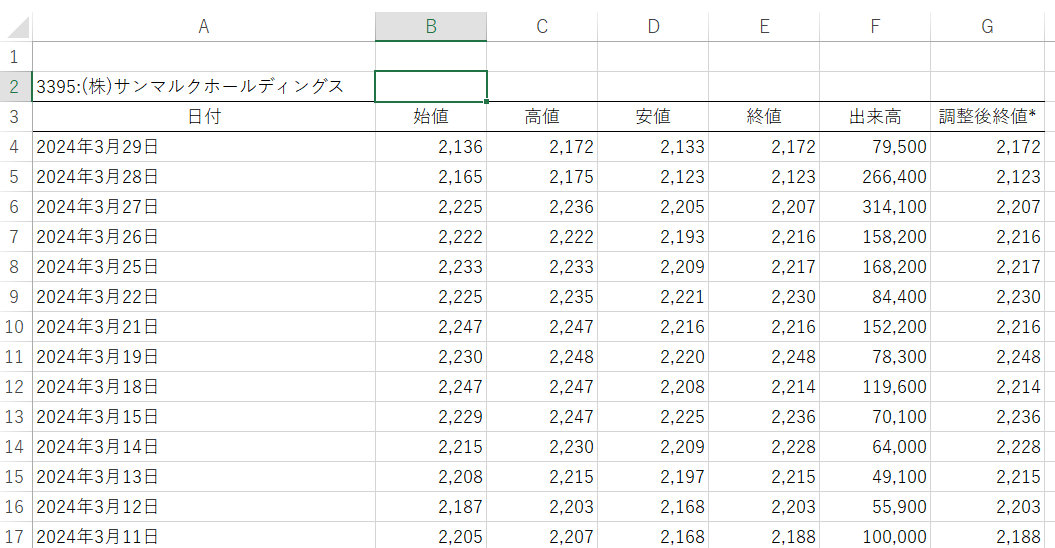
「調整後終値」とは、時系列で比較ができるように調整された株価です。例えば、1株が2株に分割されれば、価値の希薄化が生じ理論上の株価は半分になります。
実際には、分割されると低い価格から購入が可能となり需要が増加する等、理論通りの株価にはならないことも多いですが、このような分割・併合の影響を取り除いた調整後株価を利用しないと株価の連続性が分断されてしまいます。従って、調整後終値を使用します。
1年分の日時の株価をダウンロードしましたが、画像の大きさの都合上その一部のみを表示しております。
具体的な計算方法
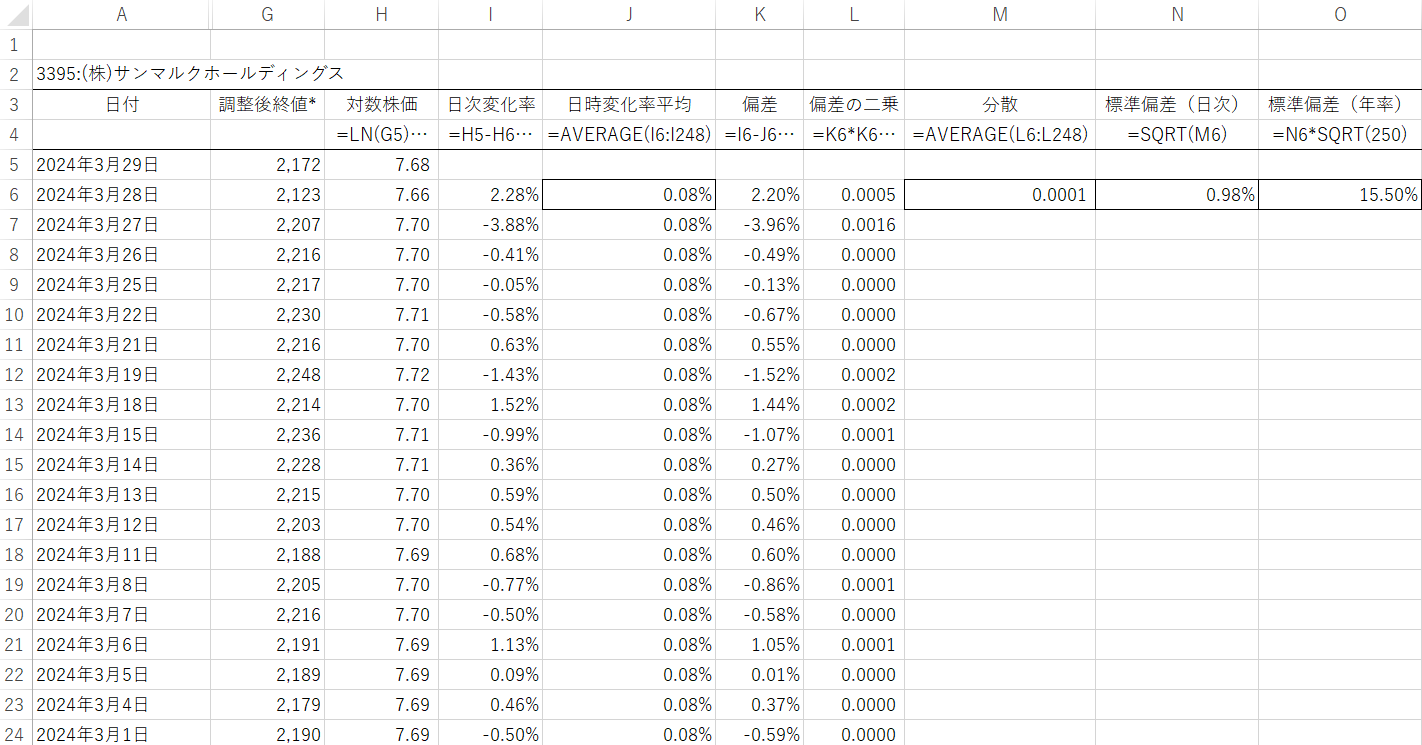
対数株価を取る(H列)
ダウンロードした「調整後終値」の自然対数を取って対数変換し、H列で対数株価を求めます。エクセルですと、「=LN」で求めることができます。
対数株価を利用する理由① 加法性が確保できる
実際の株価と、対数株価で変化率を検討します。
| 1 | 2 | 3 | |
|---|---|---|---|
| 実際の株価 | 10,000円 | 13,000円 | 10,000円 |
| 変化率 | +30% | △23% | |
| 対数株価 | 9.21034 | 9.472705 | 9.21034 |
| 変化率 | +26% | △26% |
例えば、株価が10,000円から13,000円に上がり、再び10,000円に戻った時、対数株価では変化率が正負が逆転して同じ値になり、加法性が確保できていることが分かります。このような性質は、様々な分析や演算を行う際の負担を軽減してくれます。
対数株価を利用する理由② モデル化しやすい
実際の株価の動きは極端に価格が振れることがありますが、対数変換して対数株価にすると影響が緩和されます。
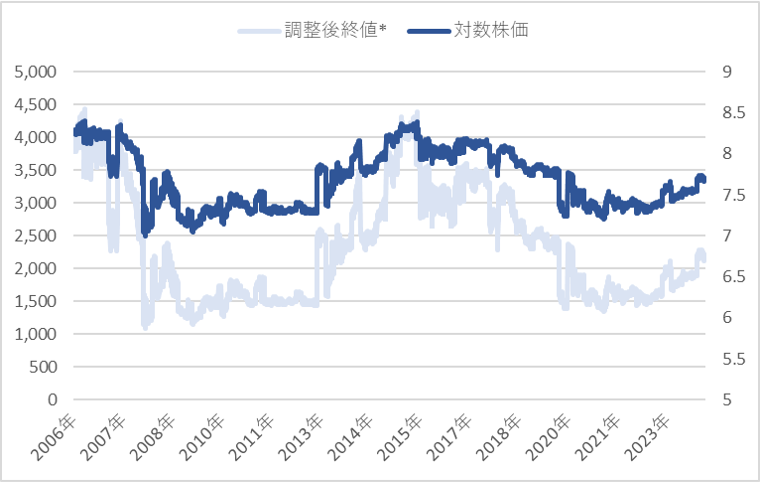
長期で見ると対数株価の方が動きが緩やかであることがよく分かります。
株価の動きはウィナー過程(ブラウン運動)から導かれたモデル等が使われますが、これらの方程式は実際の株価に現れる極端な動きを表現できていないため、対数株価を利用した方がモデル化された動きと実際の動きが近くしくなり精度が上がります。
日次の変化率を取る(I列)
I列で日次の変化率を取っています。この株価の変化率の変動の大きさを示す指標がボラティリティでした。エクセル関数「=LN(G5/G6)…」として、直接日次変化率の対数を取っても結果は同じです。
次にJ列で日時変化率の平均を取ります。
偏差、分散、標準偏差(日次)の算出
変化率の偏差(K列)
J列で求めた平均値と、各データの差が偏差です。
偏差=日次の株価変化率ー日次株価変化率の平均(0.08%)
分散(M列)
分散=$\displaystyle \sum_{}^{}$偏差の二乗×発生確率
偏差は負の値も取るため平均値からの乖離の度合いを示す指標としては使いづらく、正の値に変換するため二乗します。発生確率はどの日も同じだと考えることができるため、平均を取れば分散になります。
日次の標準偏差(N列)
標準偏差=分散の平方根
N列で標準偏差(日次)を求めています。分散は二乗したものですので単位が変わってしまい扱いづらい時もあります。よって、平方根を取って%に戻します。
ボラィテリティ(株価の変動率の標準偏差の年率)を求める
日次ベースで株価の変化率を捉え標準偏差を算出いたしました。そのため、当該標準偏差は日次の変化率のブレを示しています。
当然ながら、年単位の方が株価は大きく変動するため標準偏差も大きくなります。「株価の変動率の標準偏差の年率」と定義されるボラィテリティは、1年の営業日数を250日と仮定すると、$\sqrt{250}$を乗じて算出することができます。
この計算方法については、下記の記事をご覧ください。

